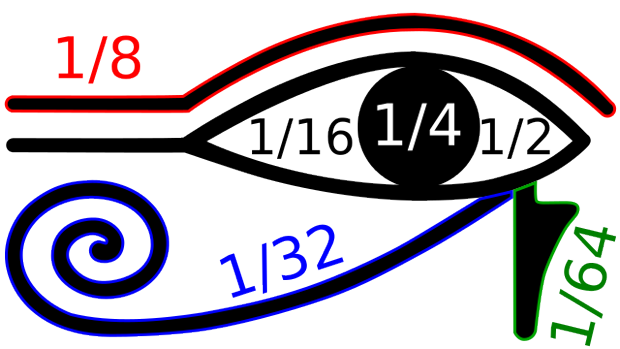
Existe la idea generalizada de que el trabajo matemático es solitario y alejado de la realidad. Es posible que muchas veces sea De esta manera Pero no es lo convencional ni, por presunto, lo más conveniente. Cualquier proyecto que se realice en Plantel, más Aún si es que Versa de un Equipo interdisciplinar, produce resultados más satisfactorios y de mayor proyección, por no platicar de que el proceso de crecimiento es más fluido y entretenido. Como ocurre en todos y cada uno de los campos de la vida profesional, son muy destacables las situaciones atípicas y extraordinarias, Siempre y en toda circunstancia llaman la atención los récords obtenidos y puede acontecer que Ciertas historias sorprendentes despierten el interés de personas ajenas a la profesión. En Matemáticas, son muy llamativos dos casos extremos de trabajo prolífico: el de Leonhard Euler (1707-1783) y el de Paul Erdös (1913-1996). Ya es muy conocida la figura de Euler, forma comunicado —o debe formar parte— de la cultura general y la recopilación de su álbum científica (más de 850 trabajos) constituye un ingente trabajo mayoritariamente individual cuyo resultado es accesible en el «Euler Archive» mantenido por la biblioteca de la Universidad del Pacífico en California, U.S.A.. Es posible que no sea tan famosa la figura de Erdös, matemático húngaro que avanzó toda su vida viajando por el mundo y colaborando de forma estrecha con la mayor volumen de colegas que pudo. En 2001, Paul Hoffman publicó una interesante biografía titulada «El hombre que Sólo amaba los números» (Ediciones Granica), resumiendo en el título la característica más significativa de este personaje. Mediante su vida, Erdös publicó, que sepamos, 1.526 trabajos de investigación en matemáticas —contando los 35 que aparecieron ahora de su fallecimiento—, la mayor comunicado en Teoría de Números y Teoría de Grupos. Más de un millar de sus trabajos acudieron efectuados en colaboración con un total de 512 coautores. Entre ellos, 202 han colaborado con Erdös en más de un artículo, siendo su compatriota András Sárközy quien ostenta el récord de 62 trabajos de investigación Conjuntos. En lo que llevamos del siglo XXI se han publicado aún cinco artículos que llevan la firma conjunta de Erdös y otro u otros creadores, trabajos que se habían iniciado en colaboración con Erdös o bien que resuelven incidentes sugeridos por él. También es posible que ciertos de estos autores quisieran lograr el tan ansiado número de Erdös idéntico a uno, reservado por la fecha a los 512 colaboradores directos, número que puede convertirse en un mérito digno de ser incluido en cualquier currículum de matemáticas. De izquierda a derecha: Paul Erdös, Ronald Graham y Fan Chung (mujer de este último) – Wikipedia El ultimo de declaraciones afortunados es Steven Butler, maestro en la Universidad estatal de Iowa, y el trabajo que posteó en 2015 —firmado conjuntamente con Paul Erdös y el últimamente fallecido Ronald Graham— merece un poco de atención. En dicho trabajo, titulado «Egyptian fractions with each denominator having three distincts prime divisors», se estudian Ciertas propiedades de las fracciones egipcias que eran desconocidas Hasta ahora. ¿Cómo? ¿Qué son las fracciones egipcias? Digamos para simplificar que son las que poseen numerador semejante a uno. ¿Por qué se llaman egipcias? Por el hecho de que en la civilización egipcia, hace más de 3.500 años, esas eran las fracciones para las que disponían de símbolos específicos y, en consecuencia, son las que se usaban para generar todas las demás. En verdad, uno de sus símbolos más representativos, el ojo de Horus, contiene las fracciones más simples con las que formaban las demás y en la 1era parte del famoso papiro Rhind, que podemos admirar en el museo Británico de Londres (Cuando nos dejen ir allí) aparece una tabla con laboriosas descomposiciones —como suma de dos, tres o bien cuatro fracciones con numerador igual a uno— de todas y cada una las fracciones del tipo 2/n para cualquier n impar A partir de 5 hasta 101 (el 3 no cuenta por el hecho de que Además disponían de un símbolo para representar la fracción 2/3). La última de ellas es muy atractiva: corresponde a la igualdad 2/101 = 1/101 + 1/202 + 1/303 + 1/606. El papiro contiene Asimismo una tabla con las descomposiciones de las fracciones n/10 para cualquier n A partir del 2 hasta el 9. Papiro Rhind – Museo Británico
Sí, yo he pensado lo mismo que tú: toda fracción 2/n se puede descomponer simplemente Así como 1/n + 1/n Pero los egipcios buscaban combinaciones donde los denominadores fueran todos diferentes. Sí, yo Asimismo Me pregunto por qué querían hacerlo De esta manera No obstante el gran matemático francés André Weil informó que la respuesta es sencilla: simplemente tomaron un sendero equivocado. Mediante la historia se han ido descubriendo muchas propiedades de las fracciones egipcias Pero Asimismo se han planteado cuestiones, Ciertas de las cuales han quedado sin resolver. Seguro que la 1era pregunta sería: ¿todas las fracciones (menores que la unidad) se pueden descomponer Del mismo modo que suma de fracciones egipcias? La respuesta es que sí y Fibonacci (c.1170-c.1250) ideó un tratamiento infalible: se resta de la fracción original la mayor fracción con numerador uno cuya diferencia es positiva; el resultado es otra fracción, menor que la 1era, a la que se aplica el mismo tratamiento; Del mismo modo que en cada paso se obtiene una volumen menor, en algún momento la diferencia es nula. En la página de Ron Knott podés descubrir una calculadora online que descompone cualquier fracción siguiendo este procedimiento. Este tratamiento va a ser infalible No obstante no Siempre y en todo momento y en todo momento da resultados «elegantes». Por ejemplo, los egipcios escribieron 2/45 = 1/30 + 1/90 y el procedimiento de Fibonacci lleva a la solución 2/45 = 1/23 + 1/1035. Hay otros ejemplos peores, lo cual alentó a la comunidad científica y, con el tiempo, se han ido desarrollando métodos más directos y eficaces. En verdad, se ha demostrado Además que cada fracción se puede descomponer De la misma forma que suma de fracciones egipcias de infinitas maneras. Una segunda pregunta podría ser: ¿cuáles son el máximo y el mínimo número de fracciones egipcias que se necesitan para descomponer una fracción dada? Se sabe que, con el tratamiento de Fibonacci, toda fracción n/m Precisa Al igual que máximo n sumandos. Los trabajos de Michael Mays en 1987 y Herta Freitag y George Phillips en 1999 proporcionan condiciones para que se alcance el número máximo de sumandos para algunos casos. Por otra parte, hasta el año 2010 se sabía que la fracción 732/733 es la de menor denominador que se puede expresar De esta manera tal y como suma de siete fracciones egipcias Pero no con seis. El matemático aficionado Hugo van der Sanden demostró ese año que 27538/27539 es la fracción más fácil que no puede descomponerse Como suma de siete Pero sí De esta forma tal como suma de ocho fracciones egipcias. ¿Cuál será la que necesite Del mismo modo que mínimo nueve fracciones egipcias? De momento, absolutamente nadie lo sabe. También que decíamos, Hay muchas cuestiones relacionadas con el tema y no todas están resueltas. ¿Qué está pasando si es que Deseamos que los denominadores sean todos pares? ¿O todos impares? Hace más de medio siglo que Erdös y Graham se preguntaban si es que se puede descomponer una fracción Así tal como suma de fracciones egipcias en las que cada denominador es producto de tres números primos diferentes. No tenemos que pensar que esa cuestión les vino a el cuero cabelludo en un arrebato de inventiva, Sino más bien más bien que venía sugerida por otros incidentes numéricos acerca de particiones en los que estaban trabajando. En el artículo que habíamos citado de Butler, Erdös y Graham, publicado en 2015, se demuestra por objetivo que todo número natural se puede escribir De exactamente la misma manera que suma de fracciones egipcias donde cada denominador es producto de tres primos diversos y hay un triple empate en las opiniones de los creadores (un voto a favor, uno en en contra de y uno en blanco) acerca de la pregunta inicial de si es que ocurre lo mismo con cualquier fracción, no necesariamente un número natural. Al similar que en la Ciencia Básica no solemos hacer el interrogante ¿para qué sirve todo esto?, nos limitaremos a proponer un sencillo problema de ingenio que podrás resolver utilizando adecuadamente lo cual acá se ha expuesto. Este es el problema: ¿cómo repartir equitativamente cinco pizzas iguales entre ocho personas? La respuesta más irreflexiva es dividir todas y cada una las pizzas en ocho porciones iguales de modo que las 40 porciones se pueden repartir De forma fácil entre las 8 personas. ¿Qué tal si es que escribimos 5/8 = 1/2 + 1/8? Al disminuir drásticamente el número de interrupciones en las pizzas, la precisión es mayor y el reparto es más justo. ¿Sería esa la manera en que los egipcios repartían los terrenos, las cosechas, las ganancias, los sueldos…? Pedro Alegría. Universidad del País Vasco/Euskal Herriko Unibertsitatea. Comisión de divulgación de la Real Sociedad Matemática Española (RSME). El ABCdario de las Matemáticas es una sección que surge de la colaboración con la RSME