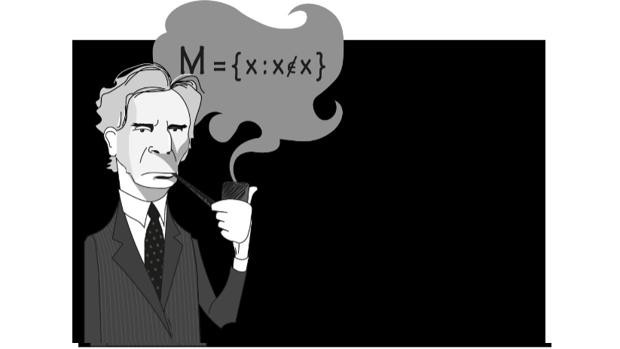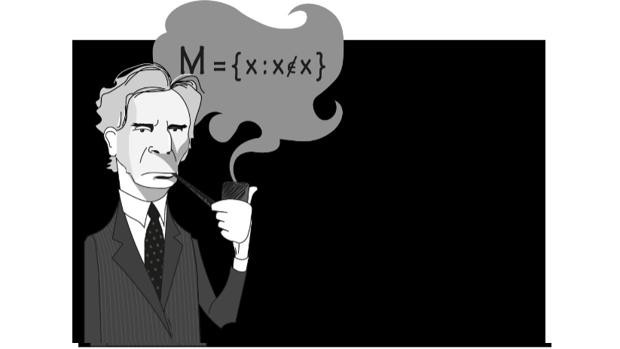Las matemáticas tienen buena reputación, son Ciertas, irrefutables, rigurosas, infalibles, casi implacables… nos referimos a ellas De exactamente la misma forma que ciencias exactas. No obstante, ¿son tan perfectas Al igual que semejan? Las matemáticas son maravillosas, Sin embargo están en construcción constante. La historia nos muestra de qué forma su progreso ha estado lleno de tropiezos, controversias y desafíos. Una de estas controversias os la contamos en un artículo precedente, en el que hablábamos del descubrimiento de las magnitudes inconmensurables por parte de los Pitagóricos, hallazgo que hizo que los griegos abandonaran en enorme medida la idea de número en favor de la geometría. Y Pese a que los números irracionales llegaron a aceptarse De esta manera tal y como números con derecho propio, la definición rigurosa de número real tuvo que esperar hasta la segunda mitad del siglo XIX. La jornada de hoy nos ocupa un desafío al que se enfrentaron las matemáticas en los primeros años del siglo XX, una sencilla paradoja que hizo que se tambaleara todo el edificio de las Matemáticas. En el siglo XIX, Comenzaron a preguntarse Algunas ideas que se daban por hecho, De exactamente la misma forma que la certeza del quinto postulado de la geometría de Euclides que asevera que por un punto exterior a una recta está pasando una única paralela. Al encontrar que considerando axiomas distintos se obtenían geometrías diversos igualmente válidas, una corriente de axiomatización se apoderó de todas las áreas de las matemáticas. En este escenario el poderoso y Asimismo influyente matemático Leopold Kronecker (1823-1891) pronunció una de las frases más célebres de la Historia de las Matemáticas: «Dios creó los números, el resto es obra del hombre». Por números se refería a los naturales, a los de tener de toda la vida, y consideraba que tanto la aritmética Del mismo modo que el análisis debían construirse Desde estos. El matemático ruso-alemán George Cantor procuró de dar una axiomática para los números naturales basándola en la teoría de Conjuntos. Cantor posteó sus ideas en 1883 con el título ‘Fundamentos para una teoría general de conjuntos’, álbum que debía Al idéntico que subtítulo ‘Una investigación matemático-filosófica acerca de el infinito’. En su obra, Cantor pedía perdón por utilizar la idea de infinito Al semejante que objeto matemático, Sin embargo Pese a ello enfureció a comunicado de la comunidad matemática capitaneada por Kronecker que alcanzó a presionar a las revistas especializadas para evitar que publicaran sus resultados. Por fortuna, Algunas figuras relevantes De exactamente la misma forma que David Hilbert y Gottlob Frege apoyaron las teorías de Cantor y este pudo ver reconocida su labor en vida. Al igual que diría Hilbert: «Nadie podrá expulsarnos jamás del paraíso que Cantor creó para nosotros». A partir de el principio, Gottlob Frege (1848-1925) tuvo claro que la teoría de Grupos de Cantor era la respuesta a la fundamentación de la matemática. Por ello se convirtió en uno de lógicos más importantes Desde Aristóteles y dedicó su vida a formalizar con absoluto rigor, con una notación exenta de ambigüedades, la teoría de Grupos iniciada por Cantor. Para Frege la capacidad humana para familiarizarse con los números naturales no podía estar relacionada con la experiencia directa o bien el espacio geométrico, Sino más bien que con el lenguaje y la lógica. Esta clase de interpretación filosófica de las matemáticas se conoce Tal y como LOGICISMO. Frege dedicó toda su vida a esta labor y en 1879 publicó su 1era gran álbum, ‘Begriffsschrift’, que podemos traducir Al igual que ‘conceptografía’, definiendo el lenguaje exacto y riguroso que necesitaba. En 1893 posteó el 1er tomo de su ambicioso proyecto ‘Grundlagen der Arithmetik’ (Fundamentos de la Aritmética). Pero en esta obra, para definir los Grupos, Frege adoptó el ‘axioma de comprensión’ que afirma que existe cualquier grupo definido por una propiedad. De un modo intuitivo definimos un grupo Al idéntico que una colección de cosas a las que llamamos elementos de expresado conjunto. Cualquier objeto al que pueda referirse la matemática es un elemento de un grupo. Existen Conjuntos de números, de libros, de gatitos, etc. Hay dos modos de acotar los elementos de un conjunto: por extensión y por comprensión. Definimos los elementos de un grupo por extensión designando a cada uno de ellos en particular. Por poner un ejemplo, el conjunto A que consta de los elementos 2, 4, 6 y 8. Este conjunto lo escribiremos como: A = {2, 4, 6, 8} Es claro que por extensión Solo podemos acotar Conjuntos con un número finito de elementos. Definimos los elementos de un grupo por comprensión expresando una propiedad que cumplan todos sus elementos. Por ejemplo, el grupo A Asimismo se puede definir como: A = { x semejantes que x es un número natural par menor que 10 }. La definición de un grupo por extensión no ofrece inconvenientes, Porque Siempre y en todo momento y en toda circunstancia tenemos una designación clara y efectiva de cuáles son sus elementos. La definición por comprensión puede volverse problemática en el caso de Grupos con un número infinito de elementos. Un ejemplo de grupo con infinitos elementos sería: P = { x tales que x es un número natural par }. Bueno, ¿y cuál es el problema? Por el hecho de que bien, ya hemos dicho que cualquier objeto es elemento de algún grupo. Particularmente, un grupo Asimismo puede ser un elemento de otro grupo. Por poner un ejemplo, podemos acotar un grupo B cuyos tres elementos sean precisamente los tres Conjuntos de números, libros y gatitos que acabamos de ver. Consideremos ahora el grupo cuyos elementos son todos y cada uno de los gatitos del mundo. Está claro que el grupo no es un gatito y por ende no es un elemento de sí mismo. Los Grupos que cumplen la condición de no ser elementos del propio grupo se llaman Grupos NORMALES. ¿No son todos y cada uno de los Conjuntos de este tipo? ¿De verdad existen Conjuntos que se contienen a sí mismo De La misma manera que elemento? Por ejemplo, pensemos en el conjunto de todos los objetos matemáticos. El propio conjunto es un objeto matemático, y por lo tanto es elemento de sí mismo. O el conjunto N de todas y cada una de las cosas que no son un gatito. Se ve Ciertamente que el grupo no es un gatito ¿verdad?, y por tanto N ha de ser un elemento de sí mismo. Los Grupos que se contienen a sí mismos Al idéntico que elementos se denominan Conjuntos SINGULARES. Además, debemos estas definiciones son exhaustivas y excluyentes: todo conjunto que podamos formar es normal o fuerte, y a su vez Solo puede ser de uno de Ambos tipos. ¡Ya estamos en predisposición de entender la paradoja de Russell! Entre tanto Frege trabajaba en el segundo tomo de sus ‘Fundamentos de la Aritmética’ un chica matemático británico llamado Bertrand Russell (1872-1970) empezó a estudiar su álbum ‘conceptografía’ y Encontró que enorme comunicado de las ideas en las que estaba trabajando ya habían sido publicadas por Frege 20 años Antes. Pese a que Russell Al igual que Frege buscaba cimentar el edificio de las matemáticas lo cual descubrió viajó más bien una carga explosiva en sus cimientos. El 16 de junio de 1902 Frege recibía una carta de Russell que contenía la paradoja que describimos ahora y que hizo que Frege parase la impresión de su segundo tomo y Además incluyese un apéndice al permanente del libro reconociendo que quizá todo el contenido de este y Además del primero eran erróneos. Russell para formular su paradoja consideró el grupo de todos y cada uno de los Grupos normales que se pueden formar. Es decir, M = { x | x no pertenece a x }. Entonces M Así tal como grupo será o bien bien NORMAL o bien FUERTE. Si es que M es normal luego M pertenece a M. Pero si M pertenece a M entonces es SINGULAR y por ende M no pertenece a M, No obstante si no pertenece a sí mismo entonces es NORMAL… y podemos permanecer Así indefinidamente. Lo que hemos visto es que M pertenece a M si y Sólo si es que M no pertenece a M lo que constituye una contradicción. Para entender mejor esta paradoja vamos a cambiar los Grupos por libros. Un cierto libro A puede ‘incluir’ a otro libro B Del mismo modo que elemento si es que en el texto del libro A se hace referencia al libro B. Imaginemos una biblioteca inmensa en la que estén todos los libros del mundo y reciba un ejemplar de cualquier libro que se escriba. El bibliotecario un buen jornada decide ordenar todos y cada uno de los libros en tan Sólo dos estanterías altísimas. En una colocará los libros que no se incluyen a sí mismo Como referencia, llamémosles libros normales. En la otra colocará los libros que se referencien a sí mismos. Por servirnos de un ejemplo, casi todo libro de matemáticas estará en esta estantería Puesto que constantemente comentan «por el Teorema A que vimos en la página X» lo cual es una referencia a sí mismo. Además ‘Alicia en el País de las Maravillas’ y ‘El Quijote’ son propiedad de este tipo. A esta clase le llamaremos libros singulares. Todos los libros que se puedan escribir deben estar en una de estas dos estanterías. ¿De verdad estamos tan seguros? Despues de ordenarlos el bibliotecario decide rellenar dos catálogos, uno para la estantería de libros normales con todos los libros de dicha estantería y otro catálogo para la estantería de libros singulares con todos los libros de la estantería pertinente. Sin embargo una vez finalizados estos dos catálogos tiene que decidir en qué estantería colocarlos. El catálogo de libros singulares lo coloca en la estantería de libros singulares añadiendo una última línea en dicho catálogo ‘Catálogo de libros singulares’. Perfecto. Dado que expresado catálogo aparece en la última línea se referencia a sí mismo y es en esta estantería donde debe estar. ¿Pero el catálogo de libros normales? Si lo coloca en la estantería de libros normales va a contar agregar una última línea que diga ‘Catálogo de libros normales’ Sin embargo luego automáticamente dejará de ser un libro normal por el hecho de que se referencia a sí mismo. De este modo que ha de estar en la estantería de los libros singulares. ¡Pero un instante! Luego no debe aparecer en la última línea del catálogo de libros normales pues no lo es. La tachamos. No obstante si es que tachamos esta línea ya no se referencia a sí mismo y sería un libro normal y debemos moverlo de estantería. Pero… ¡¡El catálogo de libros normales parece no encajar en ninguna de las dos estanterías!! ¡¿Acaso todo el edificio de las matemáticas es una mera falacia y tenemos que desamparar de confiar en ella?! Alfred North Whitehead, colaborador y amigo de Russell diría que «nunca va a haber otra vez una alegre y confiada mañana». ¡En próximos artículos sabremos si algún superhéroe matemático acudió al rescate del edificio completo de las matemáticas! Podéis ver este apasionante drama matemático en formato vídeo aquí. De la misma forma podéis descargaros el cómic de la Paradoja de Russell aquí. Urtzi Buijs es Profesor Titular del área de Geometría y Topología en la Universidad de Málaga. Miriam González es Desarrolladora de Software en la Universidad de Málaga. Los dos son fundadores del canal de Youtube Archimedes Tube. El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).